Excel-tippek VII: Évek, hónapok, napok

De mi van akkor, ha mi számolni is szeretnénk az adott nappal? Ilyenkor használhatjuk a HÉT.NAPJA függvényt, melynek első paramétere az a dátum, aminek a napjára kíváncsiak vagyunk, a második pedig az "eredmény típusa". Ez utóbbitól függ, hogy milyen nappal kezdődik a hét (1 vagy 17 vasárnap, 2, 3 vagy 11 hétfő, 12 kedd, 13 szerda stb.), illetve hogy 0-val vagy 1-gyel kezdődjön a számolás (ha 3, akkor 0-tól, minden más esetben 1-től). Így például az =A1-HÉT.NAPJA(A1;3) képlet minden esetben az A1-es cellában található dátumot megelőző hétfőt adja eredményül.

Más esetekben az is fontos lehet, hogy egy adott nap az év hányadik hetében is van. Ennek kiszámítására szolgál a HÉT.SZÁMA függvény, első paramétere a dátumérték, aminek hetére kíváncsiak vagyunk, a második attribútuma pedig egyrészt a "rendszert" határozza meg, másrészt a hét kezdőnapját. Az úgynevezett rendszer ez esetben azért fontos, mert vannak, akiknél az év első hete mindig a január 1-jét tartalmazó hét (1-17.), míg az ISO 8601 szabvány úgy fogalmaz, hogy az év első hete az év első csütörtökét tartalmazó hét vagy másképpen az a hét, amelyiken január 4. van (21). Ez utóbbit használja természetesen az ISO.HÉT.SZÁMA függvény is, aminek csak és kizárólag egy dátumértéket kell megadnunk.

Ünnepek és munkanapok

A dátumokkal kapcsolatos egyik legösszetettebb feladat, amikor munkanapokkal kell számolnunk. Szerencsére az Excel ehhez négy hasznos függvényt nyújt számunkra, az ÖSSZ.MUNKANAP és a KALK.MUNKANAP függvényeket, valamint ezek .INTL végződésű párjait.

Az ÖSSZ.MUNKANAP és a KALK.MUNKANAP függvények között az a különbség, hogy előbbinek két dátumot kell megadnunk, és eredményül a kettő közötti munkanapok számát kapjuk meg, míg utóbbinál egy kezdődátumot, valamint egy pozitív vagy negatív munkanapszám alapján kapjuk meg a másik végdátumot. Mindkét függvény opcionális paramétere egy tartomány vagy tömb, amiben az ünnepnapokat kell felsorolnunk.

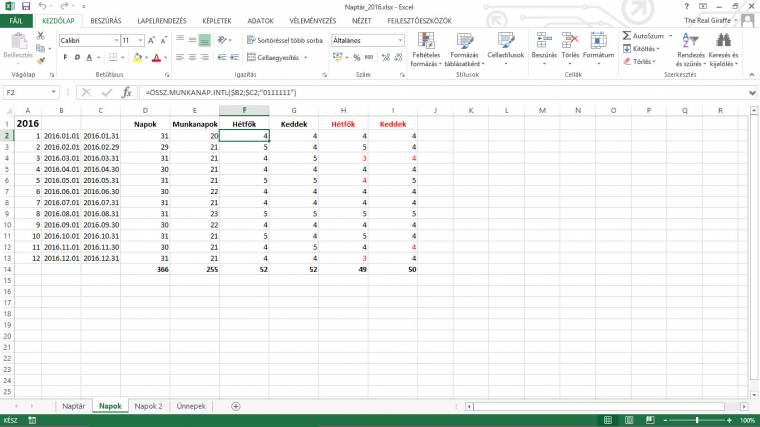
Mindkét függvényre igaz, hogy a szombatokat és a vasárnapokat nem tekintik munkanapnak. De mi van akkor, ha valakinek például a kedd és csütörtök a pihenőnapja? Ilyenkor kell elővennünk ÖSSZ.MUNKANAP.INTL és a KALK.MUNKANAP.INTL függvényeket, amelyeknél egy kód vagy egy hétkarakteres "bináris szöveg" formájában - amikor is az 1-esek a munkaszüneti napokat, a 0-k a munkanapokat jelölik, például "0101000" a fent említett kedd és csütörtök pihenőnap - megadhatjuk, hogy melyek a munkaszüneti napok. Így például azt is nagyon könnyen kiszámolhatjuk, hogy mennyi különórája lesz gyermekünknek 2016 első félévében, ha minden hétfőn és csütörtökön jár foglalkozásokra:

A képletben "Ünnepek" egy nevesített tartomány, amiben az ünnepnapokat soroltuk fel.

Húsvétszámítás

Az ünnepnapok többségének nagyon egyszerűen meg lehet határozni az időpontját, hiszen csak az évszámot kell cserélnünk a DÁTUM függvényben, például =DÁTUM(ÉV;3;15) vagy =DÁTUM(ÉV;12;25). Az egyetlen probléma a húsvéttal van, ez ugyanis úgynevezett mozgó ünnep, időpontja évről évre változik. A Nagy Konstantin által összehívott, 325-ös niceai zsinat határozata szerint a húsvéti ünnep a tavaszi napéjegyenlőséget követő holdtölte utáni vasárnapon van. Így legkorábban a húsvét március 22-én lehet, amennyiben a március 21-i tavaszi napéjegyenlőség szombatra esik, és aznap éppen telihold is van. Ez nem túl gyakran fordul elő, legutóbb ilyen korai húsvét 1818-ban volt, legközelebb pedig 2285-ben, majd 2353-ban lesz. A legkésőbbi húsvét április 25-én lehet, hogyha a holdtölte pont a tavaszi napéjegyenlőség utáni napra esik, majd az ezt követő teljes holdciklust lezáró újabb telihold vasárnap jön el, mert így még egy hetet várni kell. Érdekes módon ez valamivel gyakoribb, így történt 1886-ban és 1943-ban is, míg a következő április 25-i húsvétra már "csak" 22-évet, azaz 2038-ig kell várnunk.

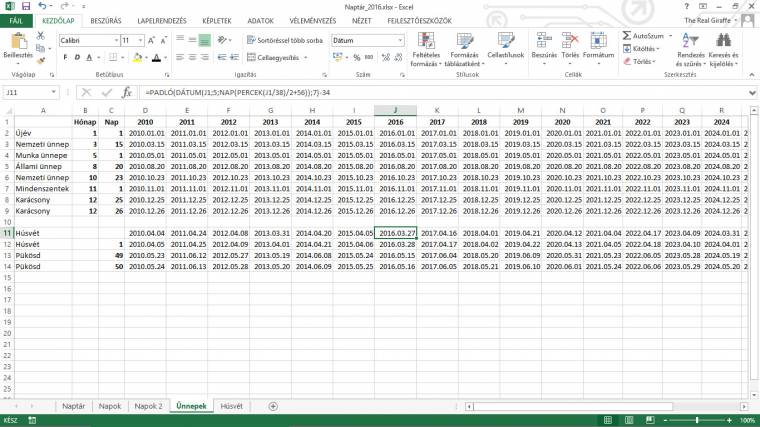
A húsvétszámítás (computus paschalis) a középkori matematika egyik legfontosabb alkalmazása volt. Az interneten keresgélve számtalan táblázatos és algoritmikus megoldást találhatunk, ám ezek részletes kifejtésétől több okból is eltekintenénk. Mi inkább Norbert Hetterich képletének (egy 2000-es Exceles verseny győztes képlete) "honosított" változatát használjuk:

Ezt a képletet az elkövetkezendő 62 évben nyugodtan alkalmazhatjuk, ugyanis először 2079-ben "téved egy hetet", majd 2203-ig megint hibátlanul működik. Ha pedig megvan húsvét vasárnap dátuma, akkor abból már egyszerűen meghatározhatjuk a húsvét hétfőét is, hiszen csak egyet kell hozzáadnunk, sőt a pünkösdvasárnapét és -hétfőét is, mivel előbbi 49, míg utóbbi 50 nappal követi a húsvétot.

- 01: Mire jó az irányítószám?
- 02: Feltételes összegek és átlagok
- 03: Kategóriák és esetszámok
- 04: Minimum és maximum értékek
- 05: Keresés a tartományokban
- 06: Automatikusan bővülő grafikonok
- 07: Évek, hónapok, napok
- 08: Formás értékek I.
- 09: Formás értékek II.
- 10: Formázások feltételekkel I.
- 11: Formázások feltételekkel II.
- 12: Új diagramtípusok

Oldalak: 1 2