Excel-tippek: Új diagramtípusok régi Excelekben
Az Excel 2016 új diagramtípusainak többségét elkészíthetjük régebbi verziókkal is - egy picit több munkával, ám több beállítási lehetőséggel.
Legutóbbi leckénkben végignéztük, milyen beállítási lehetőségei (valamint korlátai és kisebb hibái) vannak az Excel 2016 féltucat új diagramtípusának: a hisztogramnak, a Pareto-diagramnak, a dobozos ábrának, a többszintű gyűrű-, a fatérkép- és a vízesésdiagramnak. Következő leckénkben azt mutatjuk meg, hogyan lehet régebbi verziójú Excelekben is ilyen vagy hasonló ábrákat készíteni, ami ugyan némi előkészületet igényel, ám egyrészt cserébe kiküszöbölhető néhány kisebb-nagyobb (jellemzően elvi) hiba, másrészt típustól függően valamivel vagy sokkal több lehetőséget kapunk a diagramok "finomhangolására".
Hisztogram
Miként azt előző leckénkben is írtuk, a hisztogramok tulajdonképpen különböző gyakorisági adatokat ábrázoló oszlopdiagramok, így elvileg nincs más dolgunk, mint kiszámolni ezeket a gyakorisági adatokat, majd oszlopdiagramon ábrázolni az eredményt. Igen ám, de máris jön az első probléma: hogyan számoljuk ki az adatok gyakoriságát? Persze az Excelben már az ősidők óta ott van a GYAKORISÁG függvény, amit pont az ilyen és hasonló esetekre találtak ki, ezért kicsit pontosabban megfogalmazva a problémát: hogyan határozzuk meg az intervallumok számát és/vagy szélességét?
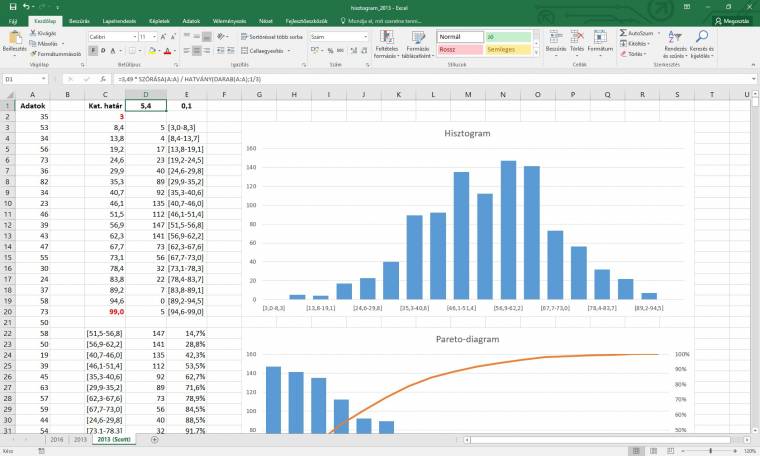
Az igazság az, hogy erre a kérdésre nincs tökéletes válasz. Persze léteznek különféle "ökölszabályok" a különböző elemszámokhoz és eloszlástípusokhoz, mint például az Excel 2016 által is alkalmazott Scott-féle szabály, de az adathalmazok többségére inkább az igaz, hogy a megfelelő osztályszám és/vagy -szélesség csak Öveges tanár úr módszerét követve, azaz "kísérletezve és gondolkodva" határozható meg.
Ebben, mármint a kísérletezésben valóban nagy segítséget jelent az Excel 2016 kategóriatengely-beállító panelje, hiszen itt - a panel szélességének megadását követően - nagyon egyszerűen módosíthatjuk az intervallumok szélességét és/vagy számát, ahogy a túl- és alulcsordulási intervallumok határait is. Ugyanakkor előfordulhatnak speciális esetek, például mikor a több nagyságrendben változó adatok "beépített lehetőségei" csődöt mondanak, amit "kézi vezérléssel" meg tudunk oldani, ez esetben logaritmikus intervallumokkal.
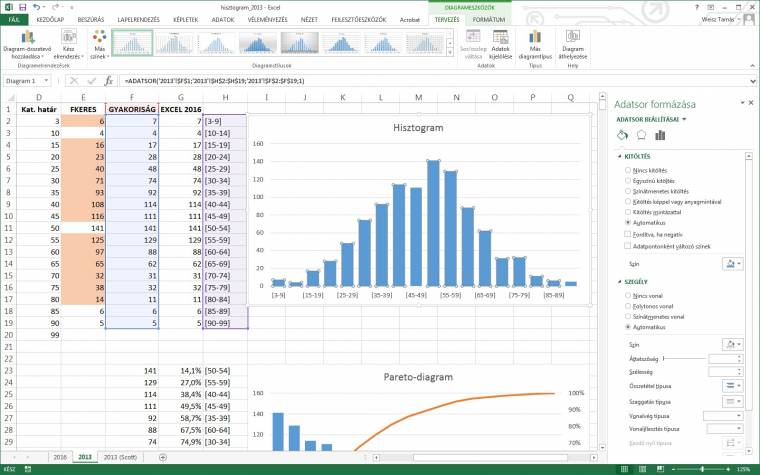
Ha (nagyon) sokat kell kísérletezgetnünk a megfelelő intervallumszám vagy -szélesség megtalálásához, érdemes megfontolni, a GYAKORISÁG függvény helyett az FKERES-DARABTELI páros használatát. Az FKERES függvénnyel egy segédoszlopban minden egyes értékhez meghatározunk egy kategóriát (akár magát az intervallumhatárt, akár egy folyamatos sorszámot használva kategóriaként), majd a DARABTELI-vel megszámoltatjuk az egyes kategóriákba tartozó elemeket.
Ez a megoldás azért egyszerűbb, még ha körülményesebbnek is tűnik, mert a GYAKORISÁG egy úgynevezett tömbfüggvény, amelynek módosítása jóval macerásabb, mint a "sima" FKERES-é és DARABTELI-é. Azt viszont nem árt tudni, hogy amíg a GYAKORISÁG-hoz az intervallumok felső határát kell megadnunk, addig az FKERES-hez az alsót (és nagyon fontos, hogy a legelső kategóriahatárnak kisebbnek vagy egyenlőnek kell lennie az adattartomány minimumával, különben az "alulcsorduló" értékeknél #HIÁNYZIK hibát kapunk), így azonos határértékeket megadva, pont a határokra eső elemek miatt a két számlálás eredménye eltérhet. Ez utóbbit azért is fontos kiemelnünk, mert az Excel 2016 értelemszerűen a GYAKORISÁG függvény algoritmusát használja az egyes intervallumokba eső értékek meghatározásához, így némi eltérés mutatkozhat, ha mi az FKERES mellett tesszük le a voksunkat.
Arra is mindenképpen érdemes odafigyelnünk, hogy ne kövessük el az Excel 2016 hibáját, és diagramunkon egyértelműen jelezzük az intervallumhatárokat. Ehhez természetesen egy plusz oszlopra lesz szükségünk, amelyben a kiválasztott függvénytől és az adatok tizedesszámától függően számoljuk ki az alsó és felső határértékeket. Ha például az intervallumhatárok tömbje a D3:D19 tartományban található, és az adatok csak egész számokat tartalmaznak, akkor az első intervallum "szövegét" a következőképpen számolhatjuk ki ="[" & (D3+1) & "-" & D4 & "]".
Ha pedig már megvannak az intervallumhatárok, ezek immáron korrekt leírásai, valamint az intervallumokba eső értékek számai, akkor nincs más dolgunk, mint utóbbi kettőt kijelölni, és létrehozni egy új oszlopdiagramot a megszokott módon ([Beszúrás] > [Diagramok] > [Oszlop- és sávdiagram beszúrása] > [Csoportosított oszlop]), majd ízlés szerint elvégezni a szokásosnak mondható beállításokat és formázásokat.
Pareto-diagram
A Pareto-diagram lényegében egy csökkenő sorrendbe rendezett hisztogram, kiegészítve egy göngyölt (kumulált) százalékot ábrázoló vonaldiagrammal. Vagyis miután az imént bemutatott módon megszámoltuk az egyes intervallumokba eső elemek számát, akkor még mielőtt létrehoznánk a diagramot, csökkenő sorrendbe kell rendeznünk az intervallumokat a bennük lévő elemek száma alapján. Igen ám, de ez nem is olyan egyszerű, mint azt elsőre gondolnánk.

