Excel-tippek: Új diagramtípusok régi Excelekben
Az Excel 2016 új diagramtípusainak többségét elkészíthetjük régebbi verziókkal is - egy picit több munkával, ám több beállítási lehetőséggel.
Folytassuk leckénket egy az utóbbi időben (ismét) népszerűvé váló diagramtípussal, az Excel 2016-ban "dobozos ábra" vagy "dobozdiagram" névre keresztelt (az angol változatban "Box and Whisker") megoldással. A dobozos grafikon nem véletlenül a statisztikai diagramok csoportjában található, ugyanis leginkább nagyobb, több száz, ezer, sőt akár milliós nagyságrendű elemi értéket tartalmazó adathalmazok eloszlásának, szimmetriájának, ferdeségének, kiugró pontjainak bemutatására alkalmas.
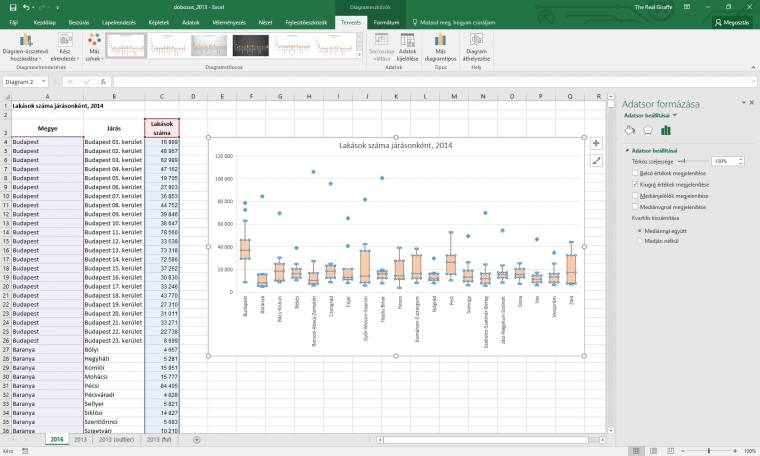
Mivel kevésbé ismert grafikontípusról van szó (ellentétben a mindenki által ezerszer látott vonal-, oszlop-, sáv- vagy kördiagramoktól), mielőtt nekikezdenénk az elkészítésének, ejtsünk pár szót arról, hogy mi micsoda a dobozos ábrán.
Teljes- és interkvartilis terjedelem
Anélkül, hogy mélyebben elmerülnénk a statisztika tudományában, röviden ismerkedjünk meg néhány fontos fogalommal, amelyekre szükségünk lesz a dobozos ábrák elkészítéséhez és persze megértésükhöz. Korábban már említettük a percentiliseket ("Mi az a percentilis?"), amelyek a rendezett adatsort száz egyenlő részre osztják, majd az ezt követően a megadott n-edik percentilis úgy bontja ketté az elemeket, hogy az adott értéknél azok n százaléka kisebb, 100-n százaléka pedig nagyobb lesz.
Az úgynevezett kvartilisek hasonlóképpen négy részre osztják a rendezett adatsort, így az első vagy alsó kvartilisnél (Q1) az adatok 25%-a lesz kisebb, 75%-a pedig nagyobb, míg a harmadik vagy felső kvartilisnél (Q3) ez pont fordítva alakul, és az adatok 75%-a lesz kisebb, 25%-a pedig nagyobb. A második kvartilis az úgynevezett medián, amely tulajdonképen a rendezett adatsor középső eleme (vagy páros számú elem esetén a két középső érték számtani közepe). A felső és az alsó kvartilis különbsége egy fontos leíró statisztikai jellemző, az interkvartilis terjedelem (IQR = Q3 - Q1), ahogyan természetesen nagyon fontos jellemzője még az adathalmazoknak a teljes- avagy mintaterjedelem, amely a legnagyobb és a legkisebb számértékek különbözete.
Bizonyos esetekben előfordulhatnak különböző mérési vagy mintavételi hibák, illetve olyan értékek, amelyek valamilyen okból jelentős mértékben kilógnak a többiek közül. Kiugró értékeknek (outliereknek) azokat az adatokat szokás nevezni - és az Excel 2016 is azokat tekinti ilyeneknek -, amelyek az interkvartilis terjedelem másfélszeresével kisebbek, mint az alsó (Q1 - 1,5 * IQR), vagy nagyobbak, mint a felső kvartilis (Q3 + 1,5 * IQR).
Segédtáblák készítése
Ahhoz, hogy létre tudjunk hozni egy dobozos ábrát, először is kategóriánként ki kell számolnunk az említett adathalmaz-jellemzőket: a minimumot, az alsó kvartilist, a mediánt, a felső kvartilist és a maximumot. Szerencsére mindegyik kiszámításához rendelkezésünkre áll egy-egy Excel-függvény, így ha csak egyetlen kategóriánk van, nincs is más dolgunk, mint ezeket használni például az első oszlopban lévő adatokra: =MIN(A:A), =KVARTILIS(A:A;1), =MEDIÁN(A:A), =KVARTILIS(A:A;3), =MAX(A:A). Akkor sem sokkal bonyolultabb a dolgunk, hogy ha az adataink kategóriánként külön oszlopban vagy sorban találhatók, hiszen ilyenkor csak az A:A-kat kell a megfelelő oszlop- vagy sorazonosítókra cserélnünk.
Valamivel bonyolultabb a dolgunk, ha a kategóriát (megye, ország, időpont stb.) egy külön oszlop tartalmazza, de tényleg csak egy nagyon picit, hiszen a jól bevált HA függvény és a "tömbösítés" ismét segítségünkre lesz: {=MIN(HA(A:A=E4;C:C))} - amikor is az A oszlopban vannak az értékek kategóriái, a C-ben az értékek, az E-ben a kategóriák listája, a kapcsos zárójel pedig azt jelzi, hogy tömbfüggvényről van szó. Sőt, miután szeretjük a kényelmet, de főleg a könnyen másolható képleteket, előkészület gyanánt az E oszlopba a 4. sortól felsoroljuk az összes kategóriát, a 3. sorba pedig F-től J-ig beírjuk a számokat 0-tól 4-ig. Ezt követően az F4-es cellába jöhet a következő képlet:

, amit a végén a Shift+Ctrl+Enter billentyűkombinációval zárjunk le. Ez először kigyűjti a C oszlopból a HA függvénnyel egy tömbbe azokat az értékeket, amelyeknek az A oszlopban található kategóriája megegyezik az első kategória azonosítójával vagy nevével, majd ezeknek kiszámolja a 0. - hiszen ezt a számot írtuk az imént az F3-as cellába - kvartilisét, ami pedig nem más, mint az adathalmaz legkisebb értéke.
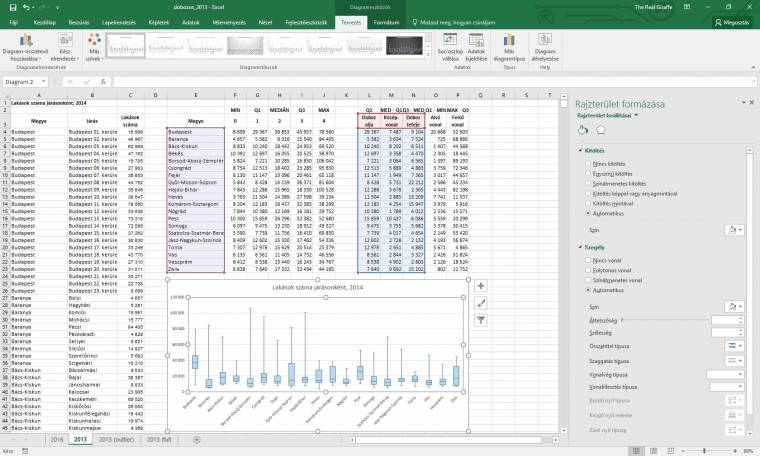
Ha most ezt a képletet elhúzzuk J4-ig, akkor már meg is van az első kategória összes szükséges adata: az 1-es alatt lesz az alsó kvartilis, a 2-es alatt a medián (ahogyan azt az elméleti bevezetőben is említettük), a 3-as alatt a felső kvartilis, míg a 4-es alatt az adott kategória legnagyobb értéke. Ha pedig kijelöljük ezt az öt cellát, majd a szokásos kis négyzetre duplán rákattintunk, megkapjuk az összes kategória összes szükséges jellemzőjét. De ezzel csak az első segédtáblánkkal vagyunk készen, a diagram létrehozásához szükségünk lesz egy másikra, amely a "relatív adatokat" tartalmazza például az L:P oszlopokban.

